“Master 7 Crucial Real Analysis Concepts: The Ultimate Course for Students”

Real Analysis is one of the most important areas in mathematics. It focuses on real numbers and the functions defined on them, helping you understand the behavior of sequences, series, limits, continuity, differentiation, and integration. Unlike basic calculus, this course emphasizes rigorous proofs and clear reasoning, giving you the foundation you need to tackle advanced problems with confidence.

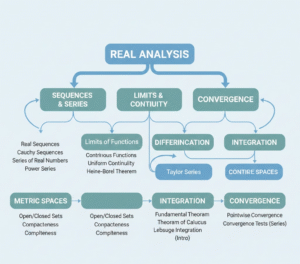
Alt text: Real Analysis Course concepts diagram

Why You Should Learn Real Analysis

Real Analysis isn’t just abstract theory—it’s a powerful tool used in mathematics, physics, engineering, economics, and computer science. By learning real analysis, you’ll develop critical thinking and analytical skills that are essential for solving complex problems and performing research in various fields.

Want to explore more? Check out Khan Academy Real Analysis Lessons
for extra practice.

What You Will Learn

This course covers 7 essential topics that form the backbone of real analysis:

Introduction to Real Numbers – Discover the structure, order, and completeness of real numbers.

Limits and Continuity – Understand how limits define function behavior and explore continuity in detail.

Differentiation – Learn the rules of differentiation and see how derivatives apply to real-world problems.

Integration – Study the Riemann integral, integration methods, and the Fundamental Theorem of Calculus.

Sequences and Series – Explore convergence and divergence with tests like the ratio and root tests.

Metric Spaces – Understand open and closed sets, and the concepts of limits and continuity in these spaces.

Function Spaces and Compactness – Learn about uniform convergence, compactness, connectedness, and important theorems like Bolzano-Weierstrass and Heine-Borel.

For deeper study, you can also visit MIT OpenCourseWare – Real Analysis.

Who Should Take This Course

This course is perfect for:

Undergraduate students studying mathematics, physics, engineering, or computer science.

Graduate students aiming to strengthen their understanding of real analysis.

Researchers needing a solid analytical foundation.

Math educators wanting to teach real analysis more effectively.

Applied scientists and engineers solving practical problems.

Data analysts and statisticians looking to enhance their mathematical skills.

Related Courses on Our Platform

Calculus Fundamentals

Advanced Mathematical Methods

By the end of this Real Analysis Course, you’ll be equipped to approach complex mathematical problems with confidence. The course combines theory, proofs, and practical examples, giving you a complete understanding of real numbers and functions.

Real-World Applications of Real Analysis

Real Analysis is not just theoretical—it has practical applications across multiple fields:

Mathematics & Physics: Provides the foundation for advanced calculus, differential equations, and modeling physical phenomena.

Engineering: Helps in analyzing signals, systems, and optimization problems with precise mathematical rigor.

Economics & Finance: Used in modeling continuous systems, understanding trends, and optimizing decision-making processes.

Data Science & Statistics: Offers a solid foundation for probability theory, statistical modeling, and understanding convergence in algorithms.

How to Excel in Real Analysis

Understand Core Definitions:

Fundamental concepts like limits, continuity, and convergence are the backbone of real analysis. Taking the time to fully understand these will make learning theorems and proofs much smoother.

Practice Proofs Consistently:

Real analysis emphasizes logical reasoning. Instead of just reading proofs, try writing your own. Start with simpler problems and gradually move to more complex ones to strengthen your analytical skills.

Use Visual Tools:

Graphs, diagrams, and charts can make abstract concepts easier to grasp. Visualizing sequences, series, and functions often clarifies complex ideas.

Connect Ideas to Calculus:

Many real analysis topics explain why the concepts you learned in calculus work the way they do. Linking these ideas helps deepen your understanding and shows their practical relevance.

Engage in Discussions:

Collaborating with peers or joining study groups can enhance your learning. Explaining concepts to others often leads to new insights and a clearer understanding.

Stay Patient and Consistent

Real analysis can be challenging initially. Regular study and persistence are key—tackling difficult problems will gradually improve your problem-solving and reasoning skills.

Why Enroll in This Course

This Real Analysis Course is more than just learning formulas—it’s about building strong analytical thinking and logical reasoning.

By completing this course, you will:

Gain a firm grasp of key topics such as limits, sequences, series, and metric spaces.

Develop confidence in writing rigorous proofs and reasoning logically.

Strengthen problem-solving and critical thinking skills, useful in academics and professional fields.

Prepare for advanced studies or research in mathematics, physics, engineering, or data science.

Whether you are a student, educator, or professional, this course equips you with the knowledge and confidence to solve complex mathematical problems with clarity and precision.